![]()
![]()
| Related Topics: | ||
Steel rods with a diameter of 0.5 +/- 0.015 inches are to be used in an application where the load is purely tensile. Investigations of the application reveal that the load is not constant in magnitude. The following tables show the typical load values and the strength data for 50 specimens.
| 10455 | 12372 | 16559 | 19703 |
| 16961 | 10595 | 10898 | 5814 |
| 17279 | 12849 | 11661 | 6795 |
| 7821 | 13017 | 11263 | 17934 |
| 6821 | 15426 | 14656 | 17703 |
| 103779 | 103633 | 103779 | 103633 | 103799 |
| 102906 | 102616 | 101162 | 107848 | 103488 |
| 104796 | 106831 | 102470 | 99563 | 102906 |
| 103197 | 102325 | 105232 | 105813 | 101017 |
| 100872 | 104651 | 103924 | 108430 | 104651 |
| 97383 | 105087 | 102325 | 106540 | 103197 |
| 101162 | 106399 | 105377 | 101744 | 105337 |
| 98110 | 100872 | 104796 | 101598 | 101744 |
| 104651 | 104360 | 106831 | 103799 | 106104 |
| 102906 | 101453 | 105087 | 100145 | 100726 |
The objective is to estimate the reliability of the steel rods against fractures.
Note: The data sets in this example use units that are not shipped with the software (inches, pounds, and pounds per square inch). If you have the "Manage other repository settings" permission, you could add these units to the repository, define their conversion factors and have them available for use for any analysis performed within the database. For the purpose of this example, it is not necessary for the software to able to convert these units to some other units, so we will use the simpler approach of setting up all the units to be in hours.
In this example, stress is defined as:
|
|
(S.1)
|
where F is the tensile load on the rod and d is the rod’s diameter. These variables are distributed. In order to obtain the stress data set, the distributions for these two variables need to be obtained first.
Let us assume that the diameters of the rods are normally distributed. The parameters of the distribution can then be determined from the given base dimension and tolerance value of the rods. Therefore, the mean of the assumed normal distribution, which is taken to be the base dimension, is 0.5 inches. The standard deviation, which is taken to be a sixth of the total tolerance value, is 0.005 inches.
To use this information, create a new Weibull++ standard folio in the project. Rename the data sheet to "Diameter." On the control panel, choose the Normal distribution and the RRX parameter estimation method. Click the Calculate icon on the Main page of the control panel. In the input window, enter 0.5 for the mean and 0.005 for the standard deviation, as shown next.
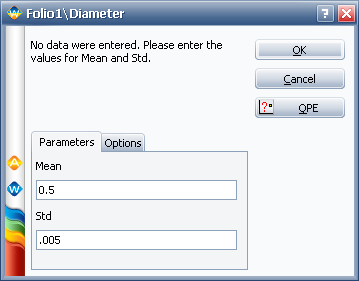
Click OK. The data sheet will be empty but the parameters of the distribution will be visible in the Analysis Summary area of the control panel.
For the distribution of the tensile load, we can use the data from Table I. Create a new data sheet in the same folio by right clicking the data sheet tab area (the area at the bottom of the window that shows the name of the data sheets) and choosing Insert Data Sheet on the shortcut menu. Rename the data sheet to "Load."
Enter the data from Table I and calculate the parameters using the 2P-Weibull distribution and the RRX parameter estimation method. The results show that the parameters of the distribution for the tensile load F are beta = 3.3435 and eta = 14278.1579 lbs, as shown next.

Now that the distributions of the variables governing Eqn. (S.1) are available, we can now obtain the stress data set. There are several conventional methods for synthesizing distributions. For this example, we will use a Monte Carlo simulation:
Open the Monte Carlo utility by choosing Home > Tools > Weibull++ Monte Carlo.
![]()
In the distribution drop-down list, choose User-Defined. Enter Eqn. (S.1) in the Equation field and click the Insert Data Source button to insert the distributions of the variables in the equation, as shown next.

Click the Settings tab. In the Data Points area, enter 1,000 and then click OK to generate the stress data set. This creates a new folio in the project. Rename the new folio to "Stress Values."
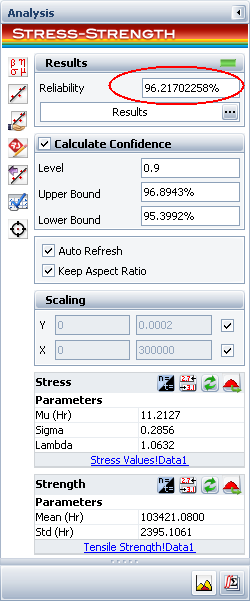
Finally, fit a distribution to the data set in the "Stress Values" folio. For this example, the distribution that best fits the stress data is a generalized gamma distribution with a mu = 11.2127 psi, sigma = 0.2856 psi and lambda = 1.0632 psi. Note that your results may vary because the data were obtained through simulation.
To obtain the strength distribution, use the tensile strength data from Table II. Create a new Weibull++ standard folio and rename it to "Tensile Strength."
Enter the data from the table in the data sheet and calculate the parameters using the Normal distribution and the RRX parameter estimation method, as shown next (showing only the first 19 rows of data).
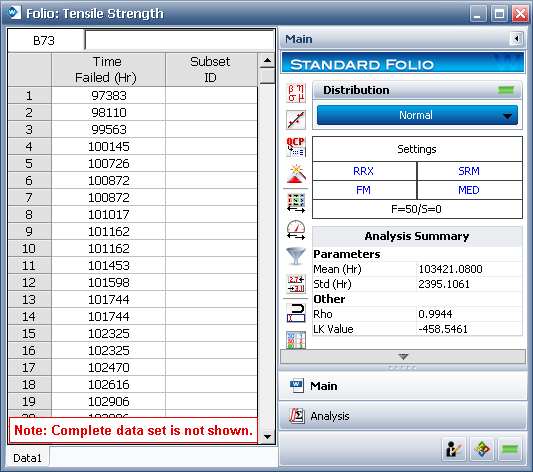
The parameters for the normal distribution of the tensile strength are mean = 103421.0800 psi and standard deviation = 2395.1061psi.
Finally, use the stress-strength folio to calculate the reliability of the steel rods. Add the folio to the project by choosing Insert > Tools > Stress-Strength.
![]()
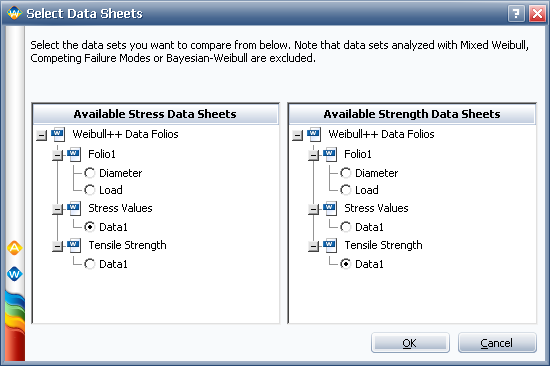
Select the data sheets containing the stress and strength data, as shown next. Click OK.
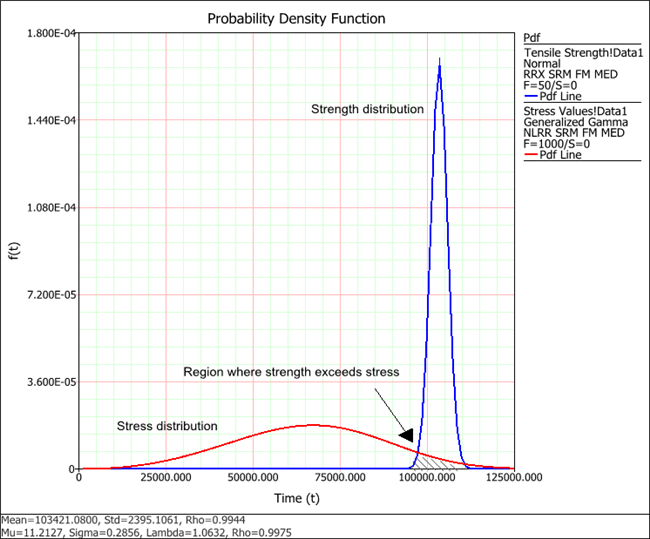
The stress-strength test shows the following plot (with the scaling adjusted and an area of the plot shaded to show the region where the strength exceeds the stress).
The result on the control panel indicates that the reliability of the steel rods against fractures is estimated to be 96.2171%, as shown next.
© 1992-2013. ReliaSoft Corporation. ALL RIGHTS RESERVED.