![]()
![]()
Description: Returns the confidence
bound for a population mean. The confidence interval is a range of values.
Your sample mean, 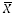 , is at the center of this range
and the range is ± CONFIDENCE. For example, if
, is at the center of this range
and the range is ± CONFIDENCE. For example, if 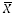 is the sample mean of delivery times for products ordered through the
mail,
is the sample mean of delivery times for products ordered through the
mail, 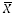 ± CONFIDENCE is a range of population
means. For any population mean, µ0, in this range, the probability of
obtaining a sample mean further from µ0 than
± CONFIDENCE is a range of population
means. For any population mean, µ0, in this range, the probability of
obtaining a sample mean further from µ0 than 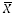 is greater
than alpha; for any population mean, µ0, not in this range, the probability
of obtaining a sample mean further from µ0 than
is greater
than alpha; for any population mean, µ0, not in this range, the probability
of obtaining a sample mean further from µ0 than 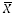 is
less than alpha. In other words, assume that we use
is
less than alpha. In other words, assume that we use 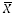 ,
Standard_dev, and size to construct a two-tailed test at significance
level alpha of the hypothesis that the population mean is µ0. Then we
will not reject that hypothesis if µ0 is in the confidence interval and
will reject that hypothesis if µ0 is not in the confidence interval. The
confidence interval does not allow us to infer that there is probability
1 - alpha that our next package will take a delivery time that is in the
confidence interval.
,
Standard_dev, and size to construct a two-tailed test at significance
level alpha of the hypothesis that the population mean is µ0. Then we
will not reject that hypothesis if µ0 is in the confidence interval and
will reject that hypothesis if µ0 is not in the confidence interval. The
confidence interval does not allow us to infer that there is probability
1 - alpha that our next package will take a delivery time that is in the
confidence interval.
Syntax: CONFIDENCE(Alpha, Standard_dev, Size)
Alpha is the significance level used to compute the confidence level. The confidence level equals 100*(1 - Alpha)%, or in other words, an Alpha of 0.05 indicates a 95 percent confidence level.
Standard_dev is the population standard deviation for the data range and is assumed to be known.
Size is the sample size.
Remarks:
All arguments must be numerical.
Alpha must be > 0 and < 1.
Standard_dev must be > 0.
Size must be an integer.
Size must be >= 1.
If we assume Alpha equals 0.05, we need to calculate the area under the standard normal curve that equals (1 - Alpha), or 95 percent. This value is ± 1.96. The confidence interval is therefore:
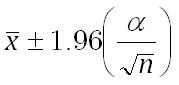
Example:
CONFIDENCE(.05, 2.5, 50) = 0.692952
© 1992-2016. ReliaSoft Corporation. ALL RIGHTS RESERVED.
 |
E-mail Link |